Предлагаю вашему вниманию программу для представления 3D координат на 2D - экране компьютера.
Когда-то хотел создать 3-мерный движок для собственной игры, но так и не дошли руки. Остался самостоятельно открытый, после многих безуспешных попыток, принцип построения 3-мерной среды. Может вам он пригодится больше, чем мне...
Программа изначально писалась на QBasic и была позднее адаптирована на Visual Basic 6. В принципе, этот алгоритм может быть легко реализован на любом языке программирования. В данной статье рассмотрим вариант с JavaScript.
Итак, начнём. Для начала надо представить что мы хотим получить. То есть, строение глаза. Условно его можно определить в виде конуса с усечённой вершиной. К этой вершине идут точки от основания конуса, попутно проецируясь на сечение (которое в нашем случае является дисплеем). Вот весь принцип, заложенный и реализованный в нижеприведённой программе. Далее его можно разложить на простые геометрические функции. Привожу код с комментариями:
<script type="text/JavaScript">
//<![CDATA[
// Устанавливаем отношение радиан к градусам.
var rad=0.0174532925199;
// Определяем размеры окна.
var reality_w=500, reality_h=500;
// 3D - 2D преобразователь
function js_3d ()
{
// Если удаление точки от экрана равно "0", то выходим из функции.
if (z==0)
{
y=reality_h-y;
return;
}
var r=0;
var ra=0;
var rp=0;
var a1=0,a2=0;
var b=0;
var c=0;
var xn=0, yn=0;
var xe=0, ye=0;
var csx=Math.floor (reality_w/2);
var csy=Math.floor (reality_h/2);
var q=1;
// Находим радиус конуса.
r=Math.sqrt (Math.pow (csx, 2)+Math.pow (csy, 2));
// Угол зрения человека составляет 120 градусов,
// следовательно угол в основании конуса будет
// составлять 30 градусов. Найдём удаление
// вершины конуса от среза (дисплея).
ra=Math.tan (30*rad)*r;
// Находим относительные, от центра, координаты точки.
xn=x-csx;
yn=y-csy;
// Находим удаление точки от центра конуса.
rp=Math.sqrt (Math.pow (yn, 2)+Math.pow (xn, 2));
// Если точка находится за "срезом"
if (z>0)
{
// Находим угол между лучом от вершины конуса
// к точке и осью конуса (треугольник: вершина
// конуса - центр основания - точка в основании).
a1=Math.atan (rp/(ra+z));
// Теперь мы знаем угол и можем найти расстояние,
// отделяющее точку в основании от высоты среза
// на основание.
b=Math.tan (a1)*z;
// Теперь удаление точки от оси минус удаление
// точки от высоты "среза" - получаем удаление
// спроецированной на "срез" точки от от оси.
c=rp-b;
}
else
{
// Всё вышеописанное, но для точки, находящейся
// перед "срезом"
a1=Math.atan (rp/(ra-z));
b=Math.tan (a1)*(-z);
c=rp+b;
}
// Теперь мы знаем как далеко отстоит от центра экрана
// проекция точки на экран. Чтобы узнать координаты
// точки на экране находим угол между этим расстоянием
// и осью X.
a2=Math.atan (Math.abs (yn)/Math.abs (xn));
// ...и находим через угол относительные (относительно
// центра) координаты XY.
if (yn!=0)
q=(Math.abs (yn)/yn);
else
q=1;
ye=Math.sin (a2)*c*q;
if (xn!=0)
q=(Math.abs (xn)/xn);
else
q=1;
xe=Math.cos (a2)*c*q;
// ...преобразуем их в абсолютные координаты на дисплее.
x=csx+Math.floor (xe);
y=csy-Math.floor (ye);
}
// Присваиваем рабочим переменным координаты точки.
var x=100, y=0, z=100;
js_3d();
alert ("x="+x+", y="+y);
//]]>
</script>
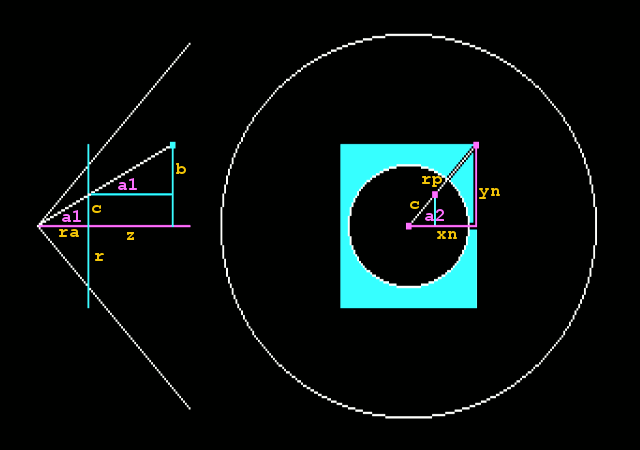
Функцию js_3d() можно использовать и не разбираясь в механизме её работы. Просто задайте перед её использованием значения переменных x,y и z и получите после выполнения координаты x и y. Для экспериментов с графикой в JavaScript можно использовать технологию "Canvas".
Вот, вроде, и всё. Спасибо за внимание.
|

 Комментировать
Комментировать